Create stunning geometric patterns with 3 simple controls:
* Swiping left and right
* Swiping up and down
* Pressing and holding.
Mathematical Overview:
A "Polar Graph" is a way of representing mathematical equations. The radius of a circle is represented with the character “r”, the angle that has been traversed around the circle is represented with the character “θ” (Theta) where 360 degrees completes a circle. So a circle with a radius of 1 has the equation: r(θ) = 1.
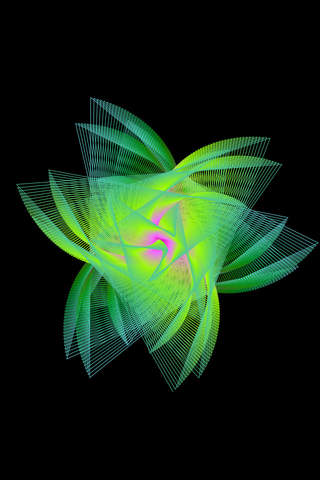
A "Polar Rose" curve is a polar graph with the equation: r(θ) = sin(kθ) As you increase the k, each increment adds to the number of “petals” that the rose has.
In Geometrics, swiping to the right will increase the number of petals by increasing k by 1 for each swipe. (The petals actually increase by 2 on even increments and decrease by 1 on odd increments)
Swiping back to the left will decrease the number of petals until you get to 1, which is the starting point circle. If you keep swiping to the left, the 2 becomes 1/2, then 1/3, then ¼ and so on(I have skipped values for k of 0 and less than 0 because a 0 k value produces a single point and the negative k values have a positive k value counterpart that produces the same picture. The roses created with fractional values are just as beautiful, have the same petal increase feature, but are not always symmetrical.
Maurer Roses: Introduced by Peter M. Maurer in his article titled “A Rose is a Rose” http://en.wikipedia.org/wiki/Maurer_rose A “Maurer Rose” is a polar rose where we skip around the figure instead of drawing it sequentially. Instead of the angle being (0,1,2,3,4,5...), we use (0,45,90,135,180,...). Swiping up increases the number of degrees we skip by 1, and swiping down decreases the skip by 1.
Pressing and holding will cycle between two modes:
* A Maurer rose that connects points to the previous point in the series.
* r(θ) = tan(kθ). Which is the same as r(θ) = sin(kθ) / cos(kθ). So as cos(kθ) approaches 0, the radius approaches infinity. This produces a very interesting pattern with no maximum radius since it goes to infinity on occasion.
As we draw the patterns, we attempt to fade through each color with a unique color fading algorithm I created. Press the menu and power buttons simultaneously to take a screen capture for use as a background or pattern.



